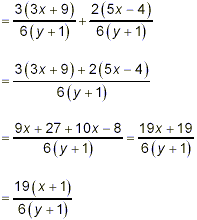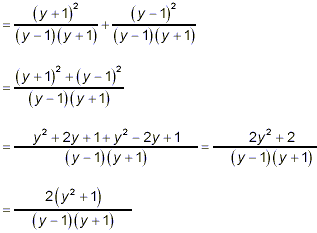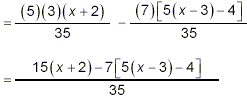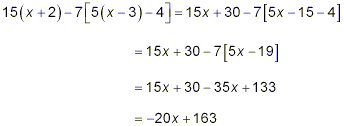Adding and Subtracting Fractions

Addition and subtraction of algebraic fractions works basically the same way as does addition and subtraction of simple numerical fractions:

(i.) rewrite all of the fractions as mathematically equivalent fractions, but having the same denominator (ideally, the simplest such common denominator).

(ii.) combine the numerators of these fractions as indicated (adding and subtracting), retaining the common denominator.

When we work with algebraic fractions, there is then often a third very important step:

(iii.) simplify the resulting fraction as much as possible. It is always necessary to make sure that once the addition/subtraction step is completed, you make a reasonable effort to simplify the result. Usually this simplification step will be made very much easier if you take care in step (i.) to make sure that you have used the simplest possible common denominator. We will illustrate the process for determining that simplest possible denominator when the fractions to be added/subtracted are algebraic fractions. You will see that the strategy is essentially the same as the strategy used to determine the least common denominator when adding or subtracting numerical fractions, except that now symbolic factors may occur as well as numerical factors.

Example 1:

Simplify

solution:

Factoring the two denominators gives:

2y + 2 = 2(y + 1)

and

3y + 3 = 3(y + 1)

so the simplest common denominator here is 3 · 2 · (y + 1) = 6(y + 1). Proceeding, we get

The numerator and denominator of this last fraction are fully factored, and there are no common factors between them to cancel. Therefore this last fraction must be the required final answer for this problem. Even if you could see that there was little possibility of cancellable common factors arising, it is desirable to write the final answer in this form with numerator and denominator fully factored.

Example 2:

Carry out the subtraction:

solution:

The denominators cannot be factored further here, so the simplest common denominator for these two fractions is their product, (2x + 5)(x + 2). We get

Since there appears to be no way to factor this numerator, this last fraction is the final answer to the original subtraction.

Example 3:

Carry out the addition:

solution:

Again, the denominators cannot be factored further, so the simplest common denominator here will be their product, (y – 1)(y + 1). Proceeding with the general strategy, we get

as the final, completely simplified answer.

Example 4:

Perform the subtraction:

solution: The denominators here are very simple – since they are prime numbers, the simplest common denominator is just their product, 35. However, we must take some care with the brackets and minus signs.

Notice particularly the use of the square brackets to ensure that the multiplication of the numerator of the second fraction by 7 really does include the entire numerator. Now that we have a single fraction, we can concentrate on simplifying the numerator. Using the principle of expanding nested brackets from innermost to outermost, we get

This cannot be factored (since the only factors in 20 are 2, 4, 5, and 10, and it is easy to see that none of these are factors of 163). So, our final answer here is