Adding and Subtracting Rational Expressions With Like
Denominators
After studying this lesson, you will be able to:
Add and subtract rational expressions with like
denominators.
- Remember that when we add or subtract fractions, we must
have a common denominator before we can add. The same is
true for adding and subtracting rational expressions.
- Once we have a common denominator, we keep the
denominator and we add the numerators. Collect like terms
in the numerator.
- Next, simplify if possible by factoring, canceling,
and/or reducing.
Example 1
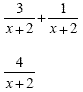 |
We have a common denominator so we can
add the numerators. This will not reduce so this is
the answer.
|
Example 2
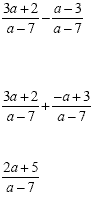 |
This is a subtraction
problem, so we have to "add the opposite"
before we do anything else. This means we will take the
opposite of everything in the numerator that follows the
subtraction sign. Now we are adding and we have a
common denominator so we keep the denominator and add the
numerators.
This will not reduce so this is the answer
|
Example 3
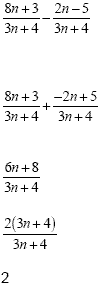 |
This is a subtraction
problem, so we have to "add the opposite"
before we do anything else. This means we will take
the opposite of everything in the numerator that follows
the subtraction sign.
Now we are adding and we have a common denominator so
we keep the denominator and
add the numerators.
This will reduce - the numerator will factor.
Cancel out the binomials 2
This is the final answer
|
Example 4
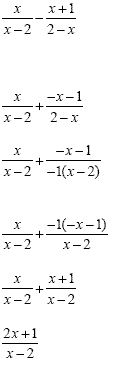 |
This is a subtraction
problem, so we have to "add the opposite"
before we do anything else. This means we will take the
opposite of everything in the numerator that follows the
subtraction sign. Now we are adding and we need a
common denominator.
Factor out -1 from the 2 - x
Move the -1 to the top and we will have a common
denominator.
Distribute the -1
Add the numerators
|
|