	Algebra Tutorials!



	Home
	Solving Quadratic Equations by Completing the Square
	Graphing Logarithmic Functions
	Division Property of Exponents
	Adding and Subtracting Rational Expressions With Like Denominators
	Rationalizing the Denominator
	Multiplying Special Polynomials
	Functions
	Solving Linear Systems of Equations by Elimination
	Solving Systems of Equation by Substitution and Elimination
	Polynomial Equations
	Solving Linear Systems of Equations by Graphing
	Quadratic Functions
	Solving Proportions
	Parallel and Perpendicular Lines
	Simplifying Square Roots
	Simplifying Fractions
	Adding and Subtracting Fractions
	Adding and Subtracting Fractions
	Solving Linear Equations
	Inequalities in one Variable
	Recognizing Polynomial Equations from their Graphs
	Scientific Notation
	Factoring a Sum or Difference of Two Cubes
	Solving Nonlinear Equations by Substitution
	Solving Systems of Linear Inequalities
	Arithmetics with Decimals
	Finding the Equation of an Inverse Function
	Plotting Points in the Coordinate Plane
	The Product of the Roots of a Quadratic
	Powers
	Solving Quadratic Equations by Completing the Square

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Solving Quadratic Equations

by Completing the Square

Recall that x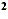 + 6 x + 9 is a trinomial square since ( x + 3 )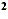 are its factors. Note that 3 is half of six.

Notes on Completing the Square

Completing the square is a procedure used to determine a solution of an equation by rewriting the equation as a trinomial square equal to a rational number.

Steps to solving quadratic equations by completing the square:

1. Isolate the variable terms on one side of the equation.

2. Divide both sides of the equation by the coefficient of x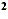 . (This is not needed if the coefficient is 1.)

3. Determine the value needed to complete the square by dividing the coefficient of x by 2 and squaring the result.

4. Add the value obtained to both sides of the equation.

5. Rewrite the trinomial as a binomial square. 6. Use the principle of square roots to determine the possible solutions and solve.