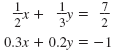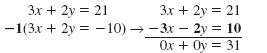	Algebra Tutorials!



	Home
	Solving Quadratic Equations by Completing the Square
	Graphing Logarithmic Functions
	Division Property of Exponents
	Adding and Subtracting Rational Expressions With Like Denominators
	Rationalizing the Denominator
	Multiplying Special Polynomials
	Functions
	Solving Linear Systems of Equations by Elimination
	Solving Systems of Equation by Substitution and Elimination
	Polynomial Equations
	Solving Linear Systems of Equations by Graphing
	Quadratic Functions
	Solving Proportions
	Parallel and Perpendicular Lines
	Simplifying Square Roots
	Simplifying Fractions
	Adding and Subtracting Fractions
	Adding and Subtracting Fractions
	Solving Linear Equations
	Inequalities in one Variable
	Recognizing Polynomial Equations from their Graphs
	Scientific Notation
	Factoring a Sum or Difference of Two Cubes
	Solving Nonlinear Equations by Substitution
	Solving Systems of Linear Inequalities
	Arithmetics with Decimals
	Finding the Equation of an Inverse Function
	Plotting Points in the Coordinate Plane
	The Product of the Roots of a Quadratic
	Powers
	Solving Quadratic Equations by Completing the Square

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Solving Linear Systems of Equations by Elimination

Use elimination to find the solution of this system.

Solution

To make the equations easier to work with:

â€¢ Clear the fractions in the first equation by multiplying both sides by 6, the LCD of the fractions.
â€¢ Clear the decimals from the second equation by multiplying both sides by 10.	10(0.3x + 0.2y = -1) → 3x + 2y = -10
To make the x-coefficients opposites, multiply the transformed second equation by -1. Add the equations.

Both variables are eliminated. The result is the false statement 0 = 31.

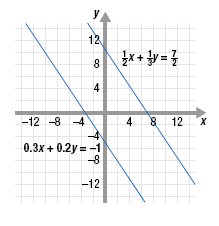
When the result is a false statement, the graphs of the equations never intersect. The graph confirms that the lines are parallel and have no points in common.

This system has no solution because the lines never intersect.

The system is inconsistent. (It has no solution.)

The equations of the system are independent. (Their graphs are not identical.)

Note â€” Solving a Linear System: Special Cases

When using either substitution or elimination, if both variables are eliminated there are two possible outcomes:

â€¢ If the resulting equation is an identity, such as 5 = 5, then the lines coincide.

The system has infinitely many solutions.

The solutions may be stated as the set of all points on the line.

â€¢ If the resulting equation is a false statement, such as 0 = 4, then the lines are parallel and never intersect.

The system has no solution.

The system is inconsistent and the equations are independent.