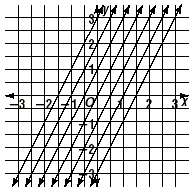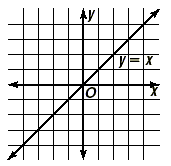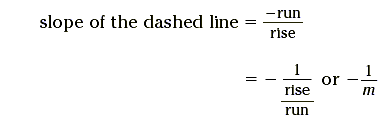Parallel and Perpendicular Lines

Objective Understand the fact that parallel lines have the same slope and that if two lines are perpendicular, then their slopes are negative reciprocals of each other.

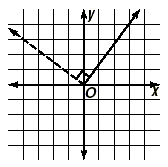
Slope and Parallel Lines

Draw the lines whose equations are y = 2x , y = 2x + 1, y = 2x + 2, y = 2x + 3, y = 2x - 1, y = 2x - 2, and y = 2x - 3.

What are the slopes of these? You can find the slopes by using one of two methods.

Method 1: Choose points on the lines.

Method 2: Recognize that the equations are in slope-intercept form, so the coefficients of x are the slopes.

Pay special attention to this second method of finding the slope. The conclusion is that all of the slopes have the value 2.

What can you say about the lines?

Key Idea

Two lines in a plane are parallel if they never meet.

If we take any two different lines in the family given above, they never meet because they "stay the same distance apart" as we move out along the lines. This example should allow you to understand the following key idea.

Key Idea

Two lines are parallel if and only if they have the same slope.

Here are some examples.

Example 1

Are the lines given by the equations 2x + 3y = 5 and 4x + 6y = 9 parallel? Why or why not?

Solution

First, write each equation in slope-intercept form.

They have the same slope, , so the lines are parallel.

Example 2

Find a line through the point at (7, 5) that is parallel to the line given by the equation y = 3x - 2.

Solution

The given line has slope 3, since it is in slope-intercept form, so we need a line of slope 3 containing the point at (7, 5). This is given by the equation in point-slope form y - 5 = 3( x - 7).

Example 3

Line m contains the points at (1, 2) and (4, 7). Line n contains the points at (0, 0) and (5, 8). Are these lines parallel?

Solution

slope of line

slope of line

Since these slopes are not equal, the lines are not parallel.

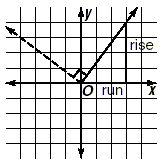
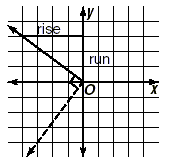
Slope and Perpendicular Lines

Perpendicular lines make a right angle with each other. Draw a pair of perpendicular lines.

If we know the slope of one of the lines, what will be the slope of the other line?

There is a very simple explanation for the answer, which we will show here.

Key Idea

If the slope of one line is m , then the slope of the other line is , the negative reciprocal of the slope of the first line.

Example 4

A line is perpendicular to the line y = x . What is its slope?

Solution

First, use the key idea. The slope of the line y = x is 1, so the slope of any perpendicular line is or -1. Draw the line y = x .

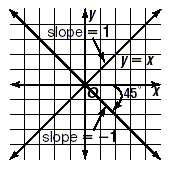
Next, draw a perpendicular line through the origin, and observe that it slopes downward at an angle of 45 degrees, and indeed has a slope of -1.

Here is a geometric explanation of the previous key idea.

Suppose there are two perpendicular lines.	To get the slope of the first line, draw a triangle whose legs are the rise and the run.	Rotate the whole figure so that the solid line is where the dashed line used to be.

It is important to note that rise and run here refer to the original rise and run of the solid line. From the graph, this means that the rise of the dashed line is the negative of the run of the solid line. (It is negative since the dashed line is sloping downwards). Also, the run of the dashed line is the same as the rise of the solid line.