|
Solving Linear Systems of Equations by GraphingOne way to find the solution of a linear system in two variables is to graph each equation on the same coordinate axes. If the lines intersect, the point(s) of intersection is the solution of the system.
Example 1 Graph each equation to find the solution of this system.
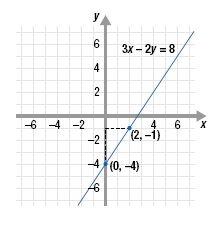
Solution To graph each equation, first write it in slope-intercept form, y = mx + b.
 This is the
ratio
To locate a second point, start at (0, -4), move up 3 (the rise) and then move right 2 (the run). Plot the new point (2, -1). Finally, draw the line through (0, -4) and (2, -1). Each point on this line represents a solution of 3x - 2y = 8.
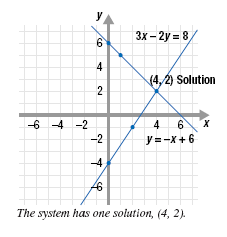
The y-intercept is (0, 6). Plot the point (0, 6). The slope is -1, which can be written as
Plot the new point (1, 5). Finally, draw the line through (0, 6) and (1, 5). Every point on this line represents a solution of y = -x + 6.
From the graph, it appears that the lines intersect at the point (4, 2). The point (4, 2) is a solution of each equation. Therefore, the solution of the system is (4, 2). Let’s verify that (4, 2) satisfies both equations.
Since (4, 2) satisfies both equations, it is the solution of the system. The solution can be written as x = 4 and y = 2, or simply (4, 2). A system that has at least one solution is called a consistent system. |
||||||||||||||||||||||||||||
To locate a second point, start at (0, 6), move down 1 (the rise) and
move right 1 (the run).
| Copyrights © 2005-2024 |