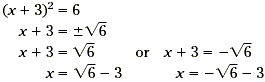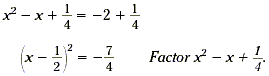Solving Quadratic Equations by Completing the Square

Those quadratic equations that are not written in the completed square form can be rewritten using the following technique.

Completing the Square

The technique of completing the square uses algebra to put any quadratic equation in completed square form. To understand how to write a quadratic expression of the form x ² + bx as a perfect square, work backwards.

( x + k ) ² = x ² + 2 kx + k ²

Notice that the coefficient of x in this expression is 2k . So, to write x ² + bx as a perfect square trinomial x ² + bx + c , let b = 2 k , or .

Example 1

Write x ² + 12x as a perfect square trinomial x ² + 12x + c , where c is a constant.

Solution

First, find . In this quadratic expression, b = 12. or 6.

Next, square this result. 6 ² = 36

Finally, add the result to the original expression. x ² + 12x + 36

This is a perfect square trinomial since x ² + 12x + 36 = ( x + 6) ² .

Completing the square is very helpful in solving quadratic equations.

Example2

Solve x ² + 6 x + 3 = 0.

Solution

Since x ² + 6 x + 3 is not a perfect square, subtract 3 from each side and then complete the square of the quadratic expression.

x ² + 6 x + 3 = 0

x ² + 6 x = -3 Subtract 3 from each side.

First, find . In the expression x ² + 6 x , b = 6. or 3

Next, square this result. 3 ² = 9

Finally, add the result to each side of the equation. x ² + 6 x + 9 = -3 + 9

Now simplify.

x ² + 6 x + 9 = -3 + 9

( x + 3) ² = 6 Factor x ² + 6x + 9.

This equation is in completed square form. Now solve by taking the square root of each side.

The method of completing the square will also let you know when there are no solutions to a quadratic equation, as shown in the following example.

Example 3

Solve x ² - x + 2 = 0.

Solution

Since the expression is not a perfect square, begin by subtracting 2 from each side of the equation to get x ² - x = -2. Then complete the square of the expression x ² - x .

First, find . In this expression, b = -1.

Next, square this result.

Finally, add the result to each side of the equation.

Now simplify.

The expression is always greater than or equal to zero because the square of any number is greater than or equal to zero. However, the right-hand side of this equation, is negative. Therefore, there can be no solutions to this equation. Thus, the original equation x ² - x + 2 = 0 has no real solution.

Try to find out what it means graphically when there are no real solutions to a quadratic equation ax ² + bx + c = 0. It means that the graph of the quadratic function y = ax ² + bx + c (a parabola) does not intersect the x-axis.

Proving the Quadratic Formula

We have seen that the method of completing the square is very useful in solving quadratic equations. It is also important in proving the Quadratic Formula.