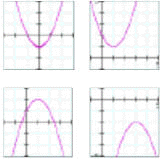
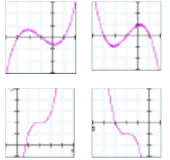
Recognizing Polynomial Equations from their Graphs

A polynomial equation is any equation that has an equation of the form:

y = c₀ + c₁·x + c₂·x² + ... + c_n·xⁿ

where the powers of x must be integers. The letters c₀, c₁, … , c_n represent numbers.

The largest power of x in the polynomial is called the degree of the polynomial.

Finding a Formula for a Polynomial Equation

Finding a formula for a polynomial equation using regression on a calculator is a two-step process. The first step consists of deciding which type of regression to use, and the second step consists of actually carrying out the regression on a graphing calculator to find the formula.

Recognizing a Polynomial from its Graph

Each of the different types of polynomial equations has a distinctively shaped graph.

Name	Typical appearance of graph	Equation (a, b, c, d, e are all constants)	Characteristics
Constant equation		y = a	Flat, horizontal graph
Linear equation		y = ax + b	Graph is a straight line
Quadratic equation		y = ax2 + bx + c	One “hump”
Cubic equation		y = ax3 + bx2 + cx + d	May have two “humps” or an “inflection point”
Quartic equation		y = ax4 + bx3 + cx2 + dx + e	May have one or three “humps” or one “hump” and an “inflection point”

Table 1: Equations and typical graphs for polynomial equations of order zero to four.