Finding the Equation of an Inverse Function
Since f(x) and f -1(x) are inverses, they “undo†each other.
For example, the function f(x) = x + 2 is a rule that says “add 2 to the
input.†The inverse of this function is f -1(x) = x - 2. This is a rule that
says “subtract 2 from the input.â€
As a consequence, the composition of f(x) and f -1(x) simplifies to x.
Property — Composition of a Function and Its Inverse
If a function, f(x), has an inverse, f -1(x), then:
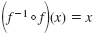 for every x in the domain of f, and for every x in the domain of f, and
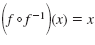 for every x in the domain of f
-1. for every x in the domain of f
-1.
Example 1
Given f(x) = 5x - 4 and
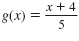 ,
determine if g(x) is the inverse
of f(x). ,
determine if g(x) is the inverse
of f(x).
Solution
If g(x) is the inverse of f(x), then the composition (f
○ g)(x) will equal x.
| Find (f ○ g)(x). |
(f ○ g)(x) |
= f[g(x)] |
Replace g(x) with
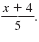 |
|
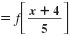 |
In f(x), replace x with
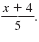 |
|
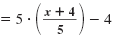 |
| Cancel common factors of 5.
Subtract. |
|
= x + 4 - 4 = x |
Since (f ○ g)(x) = x, g(x) is the
inverse of f(x).
Note:
We can also use (g ○ f)(x) to see if
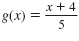 is the inverse of f(x)
= 5x - 4. is the inverse of f(x)
= 5x - 4.
|